ไม่เหมือนกับ ค่าเบี่ยงเบนมาตรฐาน คือรากที่สองของค่าตัวเลขที่ได้รับขณะคำนวณความแปรปรวน หลายคนเปรียบเทียบแนวคิดทางคณิตศาสตร์ทั้งสองนี้ ดังนั้นบทความนี้พยายามที่จะอธิบายความแตกต่างที่สำคัญระหว่างความแปรปรวนและค่าเบี่ยงเบนมาตรฐาน
แผนภูมิเปรียบเทียบ
| พื้นฐานสำหรับการเปรียบเทียบ | ความแปรปรวน | ส่วนเบี่ยงเบนมาตรฐาน |
|---|---|---|
| ความหมาย | ความแปรปรวนเป็นค่าตัวเลขที่อธิบายความแปรปรวนของการสังเกตจากค่าเฉลี่ยเลขคณิต | ค่าเบี่ยงเบนมาตรฐานคือการวัดการกระจายตัวของการสังเกตภายในชุดข้อมูล |
| มันคืออะไร? | มันคือค่าเฉลี่ยของการเบี่ยงเบนกำลังสอง | มันคือค่าเบี่ยงเบนกำลังสองเฉลี่ยของรูท |
| ติดป้ายว่า | ซิกมาสแควร์ (σ ^ 2) | ซิกมา (σ) |
| แสดงไว้ใน | หน่วยกำลังสอง | หน่วยเดียวกับค่าในชุดข้อมูล |
| บ่งชี้ว่า | ไกลแค่ไหนที่บุคคลในกลุ่มจะกระจายออกไป | การสังเกตของชุดข้อมูลแตกต่างจากค่าเฉลี่ยเท่าใด |
นิยามของความแปรปรวน
ในสถิติความแปรปรวนหมายถึงการวัดความแปรปรวนที่แสดงถึงจำนวนสมาชิกของกลุ่มที่จะถูกกระจายออกไป พบระดับเฉลี่ยที่การสังเกตแต่ละครั้งแตกต่างจากค่าเฉลี่ย เมื่อความแปรปรวนของชุดข้อมูลมีขนาดเล็กก็จะแสดงความใกล้ชิดของจุดข้อมูลไปที่ค่าเฉลี่ยในขณะที่ค่าความแปรปรวนมากขึ้นแสดงให้เห็นว่าการสังเกตจะแยกย้ายกันไปรอบ ๆ ค่าเฉลี่ยเลขคณิตและจากกันและกัน
สำหรับข้อมูลที่ไม่จัดประเภท :
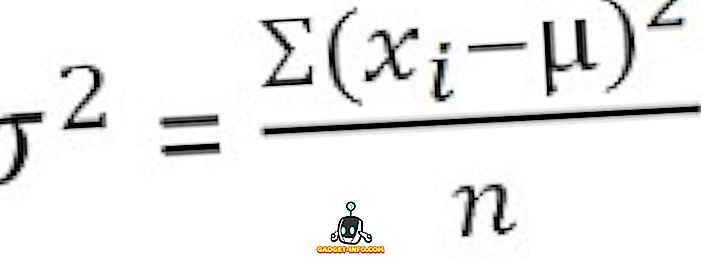
สำหรับการแจกแจงความถี่ที่จัดกลุ่ม :
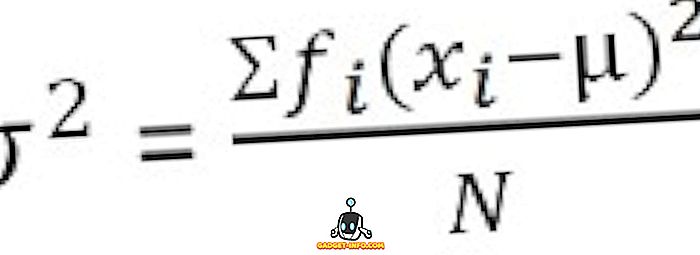
คำจำกัดความของส่วนเบี่ยงเบนมาตรฐาน
ค่าเบี่ยงเบนมาตรฐานคือการวัดที่คำนวณปริมาณการกระจายตัวของการสังเกตในชุดข้อมูล ค่าเบี่ยงเบนมาตรฐานต่ำเป็นตัวบ่งชี้ความใกล้ชิดของคะแนนกับค่าเฉลี่ยเลขคณิตและค่าเบี่ยงเบนมาตรฐานสูงแทน คะแนนจะกระจายไปทั่วช่วงของค่าที่สูงขึ้น
สำหรับข้อมูลที่ไม่จัดประเภท :

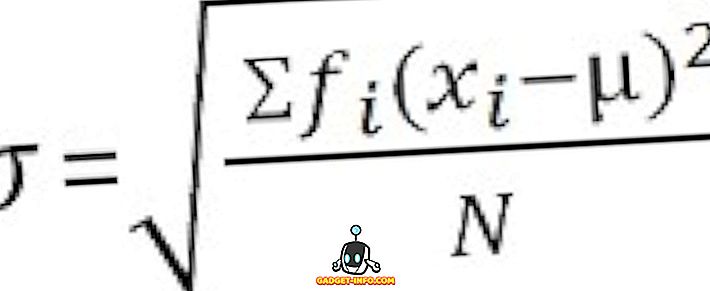
ความแตกต่างที่สำคัญระหว่างความแปรปรวนกับค่าเบี่ยงเบนมาตรฐาน
ความแตกต่างระหว่างส่วนเบี่ยงเบนมาตรฐานและความแปรปรวนสามารถวาดได้อย่างชัดเจนในพื้นที่ดังต่อไปนี้:
- ความแปรปรวนเป็นค่าตัวเลขที่อธิบายความแปรปรวนของการสังเกตจากค่าเฉลี่ยเลขคณิต ค่าเบี่ยงเบนมาตรฐานคือการวัดการกระจายตัวของการสังเกตภายในชุดข้อมูล
- ความแปรปรวนคืออะไรนอกจากค่าเบี่ยงเบนกำลังสองเฉลี่ย ในทางกลับกันค่าเบี่ยงเบนมาตรฐานคือส่วนเบี่ยงเบนสแควร์รูท
- ความแปรปรวนถูกแสดงโดย sigma-squared (σ2) ในขณะที่ค่าเบี่ยงเบนมาตรฐานถูกระบุว่าเป็น sigma (σ)
- ความแปรปรวนจะแสดงเป็นหน่วยสี่เหลี่ยมซึ่งมักจะใหญ่กว่าค่าในชุดข้อมูลที่กำหนด ตรงข้ามกับค่าเบี่ยงเบนมาตรฐานซึ่งแสดงในหน่วยเดียวกับค่าในชุดข้อมูล
- ความแปรปรวนวัดระยะห่างของบุคคลในกลุ่มที่จะกระจายออกไป ในทางกลับกันส่วนเบี่ยงเบนมาตรฐานจะวัดว่าการสังเกตของชุดข้อมูลแตกต่างจากค่าเฉลี่ยเท่าใด
ภาพประกอบ
คะแนนที่นักเรียนทำในห้าวิชาคือ 60, 75, 46, 58 และ 80 ตามลำดับ คุณต้องหาค่าเบี่ยงเบนมาตรฐานและความแปรปรวน
ก่อนอื่นคุณต้องหาค่าเฉลี่ย

ดังนั้นเครื่องหมายเฉลี่ย (หมายถึง) คือ 63.8
คำนวณความแปรปรวน
| X | (xA) | (XA) ^ 2 | |
|---|---|---|---|
| 60 | 63.8 | -3.8 | 14.44 |
| 75 | 63.8 | 11.2 | 125.44 |
| 46 | 63.8 | -17.8 | 316.84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | 16.2 | 262.44 |
โดยที่ X = การสังเกต
A = ค่าเฉลี่ยเลขคณิต
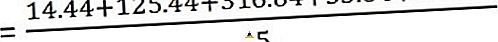
และค่าเบี่ยงเบนมาตรฐานคือ -

ความคล้ายคลึงกัน
- ทั้งความแปรปรวนและค่าเบี่ยงเบนมาตรฐานเป็นค่าบวกเสมอ
- หากการสังเกตทั้งหมดในชุดข้อมูลเหมือนกันค่าเบี่ยงเบนมาตรฐานและความแปรปรวนจะเป็นศูนย์
ข้อสรุป
ทั้งสองนี้เป็นคำศัพท์ทางสถิติพื้นฐานซึ่งมีบทบาทสำคัญในภาคต่าง ๆ ค่าเบี่ยงเบนมาตรฐานเป็นที่ต้องการมากกว่าค่าเฉลี่ยเนื่องจากมีการแสดงในหน่วยเดียวกับค่าที่วัดในขณะที่ค่าความแปรปรวนจะแสดงในหน่วยที่มีขนาดใหญ่กว่าชุดข้อมูล